シミュレーションで得た実測値を元に理論値を推測する方法。あるいは信頼水準とその区間について。

例えば、銀行窓口の平均待ち時間が5分であるモデルを用いてシミュレーションを何回か行った場合、その待ち時間の実測値は(実装にミスがなければ)5分に収束すると予想されます。

それでは、逆にあるシミュレーションを行った結果、平均待ち時間が5分だったとして、それを元にしてこのモデルでは平均待ち時間は5分である、と言えるでしょうか？あるいはそのように主張する場合、どうすればより説得力を持たせることができるでしょうか？

シミュレーションでできること

シミュレーションは理論上のモデルだけでは計算するのが難しいパラメータを実際に計測するのに便利です。

例えば先の銀行窓口の例で言うならば、単位時間あたりの顧客数がポアソン分布だとか、各窓口の平均処理時間が指数分布だとかは簡単にモデル化することができます。しかし、そのモデルにおける各顧客の平均待ち時間などという表にでてこないパラメータを計算だけで取得するのはそれほど簡単ではありません。(まあ、この例では簡単かもしれませんが、言いたいことは伝わるかと)

そんなときにシミュレータをモデルに沿って構築すれば、そのようなモデルには直接出てこない数値を実測することができます。平均待ち時間ならば、シミュレーションの最中に各顧客の待ち時間をそれぞれ記録しておいて、終了後にそれらの平均を取ればいいのです。

実測値=理論値？

さてここで問題が出てきます。シミュレーションの実測値はあくまで一つの結果でしかありません。シミュレーションの結果がそうであったからといって、理論上のモデルでもそうなるに違いないと結論付けることができるでしょうか？

例えば多くの場合、シミュレーションには擬似乱数を使うでしょうから、その結果は完全ランダムにはなりません。一方、モデル上で乱数といえば完全ランダムを指すので、ここに齟齬が生じます。

それならば、と何回もシミュレーションした結果の平均をとってみるとどうでしょうか。回数が多くなればなるほど、実測値の平均=理論値であるという説得力が多くなるような気がします。それでは実際どのくらいの試行回数が必要なのでしょうか。

ある偉い人が提唱した大数の法則では次のように言われています。

式1：

ここで、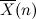は実測値n回の平均、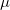は理論値の平均を表します。つまり、無限回試行した実測値の平均は理論値として扱ってもいいことになります。

時は金なり

とはいえ、シミュレーションを無限回やろうとする人はいないでしょう。なんとか有限時間内に収めたいものです。そこでまたまたある偉い人が中心極限定理というものを見つけました。

式2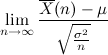：の分布は正規分布に近似する。

ここで、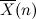と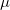は先ほどと同じ、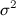は理論値の分散を表します。

これはどういうことかというと、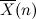がどのような分布をとるかどうかにかかわらず、それを変形した式2の極限の分布は標準正規分布になるということです。標準正規分布とは平均が0、分散が1となるような分布です。

標準正規分布は完全にモデル化することができるので、次のような情報も計算することができます。

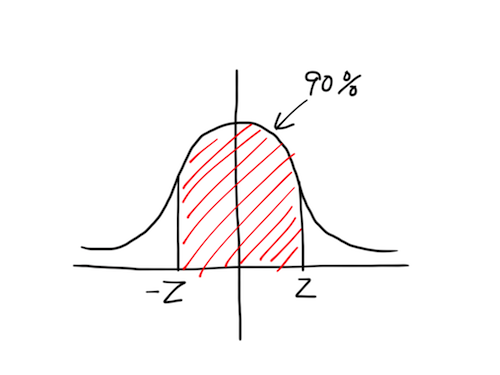
赤の斜線は標準正規分布に沿った変数の値が-zからzの範囲になる時の確率を表します。この場合90%の確率でその範囲に収まるということがわかります。先ほどの変数を用いた式で表すと、

式3：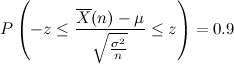

となります。これを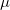について変形すると、

式4：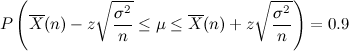

これは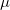が区間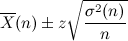内にある確率が90%であると読み替えることができます。このような区間を信頼区間と呼び、その確率を信頼水準または信頼係数と呼びます。改めて式を見てみると、実測値から得た理論値の信頼性とその上限及び下限を同時に示していることになります。

ここまでをまとめてみましょう。今回の目的は理論値を実測値から推定することでしたが、100%完璧に推定するためには無限回の試行が必要だとわかりました。そこで式の変形と標準正規分布を利用して、理論値がある一定の信頼水準を持つという区間を求めることにしました。

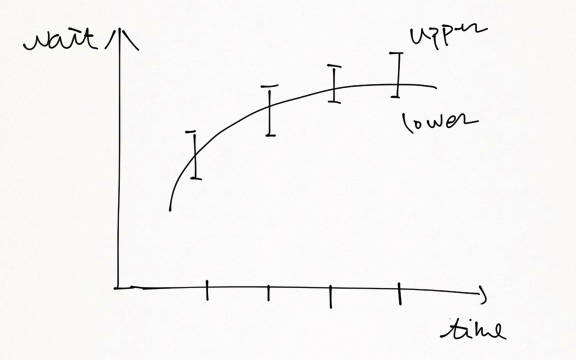
まず信頼水準を決めます。実際は90~95%が使われるとのことです。次に標準正規分布表を用いて、標準正規分布に沿った変数がある区間に存在する確率が信頼水準となるような区間(-z,z)を求めます。zが見つかればあとは式4に基いて実際の上限と下限を計算するだけです。このような評価を行ったグラフを提示する場合、以下のように上限と下限の範囲を示すことで、理論値の「あそび」を可視化することができます。

いくつかの制限

このような信頼水準と区間を用いた手法は、ただ実測値の平均を示すよりも説得力があることは確かです。しかし、それでも信頼水準があくまで確率である以上、理論値がその区間外にある確率もまた0ではありません。(理論値がある区間に100%の確率で存在するということは、その区間は(-無限,無限)である必要がある)。その他にもいくつか問題があります。

一つめは、式2が完全に正規分布と一致するには無限回の試行を必要とします。これは無理なので、nを十分に大きくしてできるだけ正規分布に近づくようにします。古い教科書では少なくとも30回以上としていますが、計算能力が発達した今日のコンピュータでは一つのシミュレーションにつき100回、1000回の試行はそれほど難しくないはずです。

もう一つは、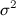です。理論値の平均を求めようとしているのに、その理論値の分散が必要になってしまいます。理論値の分散も未知の場合がほとんどなので、実際の手順では実測値の分散で置き換えるしかないとのことです。

まとめ

シミュレーションは計算モデルでは簡単に計算出来ないようなパラメータを実測するのに便利ですが、果たしてその実測値がどのように理論値と関連するかを示すことが必要です。今回は実測値を元にある信頼水準を満たすような区間を計算する方法を学びました。

上記の制限のおかげで、これらの区間はあくまでも近似値ということに注意する必要があります(t分布を用いた手法など、ある条件のもとで近似でない値を示すことのできる方法もある)。しかしながら、信頼水準と区間を示すことはシミュレーションを用いたモデル評価においては最低限のマナーであるといえるでしょう。