条件付き確率と独立性について

52枚のトランプセット(ジョーカーを除く)から続けて二枚カードを引いた時、両方とも絵柄(J、Q、K)のカードである確率を求めなさい。

最初に52枚から12枚を選び、その後51枚から11枚を選ばなければいけないので、その確率は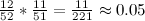でおよそ5%となります。

条件付き確率

最初に絵柄のカードを1枚引いているのだから、その後の確率が影響をうけるのは自然なことにように見えますが、このように事象Aが起こったと仮定して、更に事象Bが起こる確率を条件付き確率と呼び、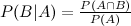と定義されます。次のベン図を見てください。

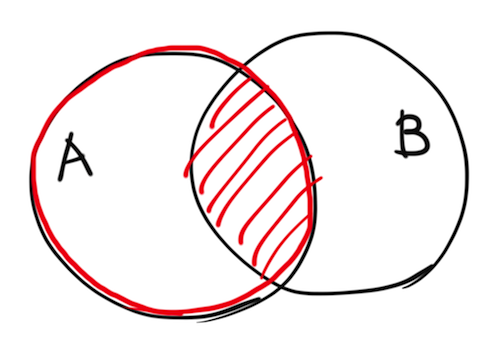
まず事象Aが起こったと仮定するので、分母は事象Aの確率そのものになります(赤の円)。その上で事象Bが起こらなければならないので、分子は赤の斜線部分、すなわち「AかつB」の確率です。

両辺に事象Aが起こる確率P(A)を掛けて、式をちょっと変更してみると、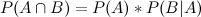となり、AかつBの確率を得ることができます。先ほどの問題に戻ってみましょう。

この場合P(A)が「最初に絵柄を引く」確率です。そしてP(B|A)が「Aが起こったとして、次に絵柄を引く」確率となります。それらをかけ合わせているので「AとBが両方起こる」確率を計算できていることがわかります。

事象の独立性

事象AとBが独立であるとします。それらはお互いに影響を受けないわけですから、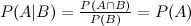になります。さらに独立な事象AとBが共に起こる確率は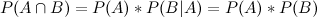です。これらを使うとある2つの事象が独立であるかどうかを確かめることができます。

例題1、2つのサイコロX、Yを同時に振る。事象Aを「サイコロXが奇数」、事象Bを「サイコロYが偶数」とするとき、AとBは独立か？

まずそれぞれの確率を計算します。事象Aの確率は2分の1。事象Bの確率も2分の1なので、これらが独立であるためにはAとBが同時に起こる確率が4分の1でなければなりません。奇数と偶数の組み合わせは(1,2)、(3,2)、(5,2)、(1,4)、(3,4)、(5,4)、(1,6)、(3,6)、(5,6)の9通りで、確率は36分の9、約分して4分の1になります。したがって事象Aと事象Bは独立であるとわかります。

例題2、互いに排他的な事象AとBがあり、事象Aが起こる確率P(A)が0<P(A)<1のとき、事象AとBは独立か？

AとBは排他であるので、AとBが同時に起こる確率は0です。一方でBが起こる確率は問題文より1-P(A)>0なので、P(A)*P(B)>0。したがってAとBは独立ではありません。

「互いに排他的」と文章で書くと両者に接点がなく、それぞれ独立であるように思えますが、確率論的には全く独立ではありません。むしろべったりです。コインの裏がでる確率はコインの表が出る確率に影響をうけることを考えるとわかりやすいかもしれません。

まとめ、あるいはハイジャック犯と乗り合わせる確率

これまで条件付き確率と事象の独立性について書いてきました。条件付き確率は日常でも無意識に活用している場面も多いと思います。しかし、それらの事象が独立であるかどうかには気をつけないといけません。最後に、統計的独立性について次のようなジョークを見つけたので引用してこの記事の結びにしたいと思います。

あなたが旅行で飛行機に乗るとして、爆弾を持ったハイジャック犯と同じ飛行機に乗り合わせてしまう危険を避けるにはどうしたらよいか？答えは、あなたも爆弾を持って乗り込む、である。ある飛行機に爆弾を持った人間が一人乗っている確率をpとすると、爆弾を持った人間が二人乗っている確率は、統計的独立性から p×pとなる。明らかに p <<1 であるから、p×p は無視しうるほどに小さくなるであろう。よってあなたは安心して旅行ができる！ -- kakuritu