モンテカルロ法を用いた待ち行列モデルのシミュレーションについて

待ち行列のシミュレーションというと、顧客が何時何分に列に並んで、何分待って、窓口の処理に何分かかったか、など時間を軸にすることが多いです。一方で、時間の概念を一切使用しない、単純に乱数と確率のみを用いるモンテカルロ・シミュレーションを待ち行列モデルに応用したものを授業で習ったので紹介します。

モンテカルロ・シミュレーションでπを求める

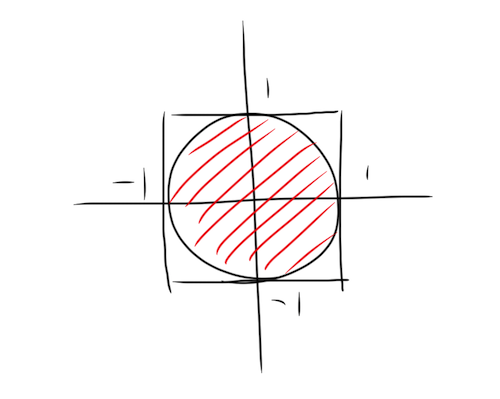
モンテカルロ・シミュレーションでおそらくもっとも有名なのは、円周率πの近似値を求めるものではないでしょうか。xy座標の中心に縦横長さ2の正方形を置き、さらにその中に半径1の円を描きます。乱数生成器を用いてx座標とy座標をそれぞれ生成し、その点(x,y)が円の内側にある、つまり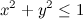になった回数をcとします。乱数が均一に(-1,1)の範囲の数値を生成すると仮定すると、点の総数Nが十分大きいとき、cとNの比は円と正方形に面積の比に等しくなるはずです(各点がまんべんなく正方形内に散らばってるのをイメージしてください)。円の面積:正方形の面積=π:4=c:Nなので、π=4c/Nが導けます。

というわけでJavaで書いてみました。

public static void main(String[] args) {
    Random r = new Random();
    int N = 100000000;
    int c = 0;
    for(int i = 0; i < N; i++){
        float x = r.nextFloat()*2-1;
        float y = r.nextFloat()*2-1;
        if(x*x + y*y <= 1){
            c++;
        }
    }
    System.out.println(4.0*c/N);
}

実行するとπの近似値が表示されるはずです。Nの数値は適当に大きくしてください。

モンテカルロ・シミュレーションで待ち行列のブロック率を求める

さて、これを待ち行列に応用してみます。顧客が1単位時間の間に列に並ぶ頻度(例えば、10分間で3人並ぶのならば0.3人/分)を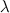とし、カウンターでの処理が終わって列から離れる頻度を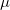とします。列に並べるのは5人まで、としましょう。すると並んでいる顧客の数に注目した以下の図を導くことができます。

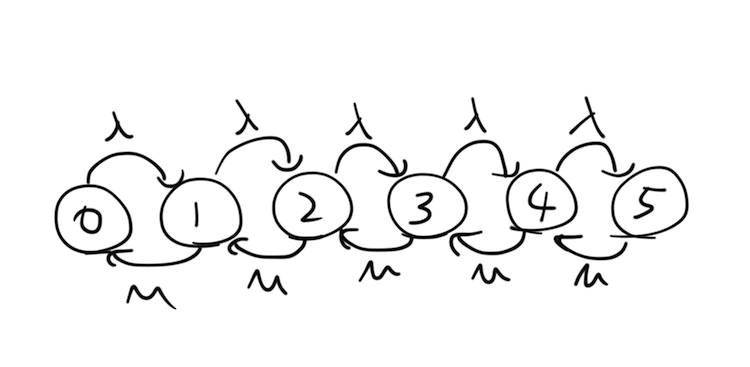
これはBirth–death processという手法で、ある状態からその隣の状態に移る頻度を表したものです。この場合、列に並んでいる顧客の数がn人の時、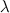の頻度でn+1人になり、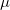の頻度でn-1人になることを表します。

一般的なシミュレーションでは、それぞれイベントを単位時間あたりの頻度に応じて発生させ、その変化を記録するものですが、モンテカルロ・シミュレーションでは上でも上げたように時間の概念がありません。つまり単位時間あたりの頻度は意味をなしません。そこで次のように考えます。

仮にあるイベントが起こったとして、そのイベントがArrival(顧客の到着)であるかDeparture(顧客の離脱)であるかを後から決めようじゃないか。もし、Arrivalだったら並んでいる顧客の数を増やし、Departureだったら減らせばいい。

イベントが発生したのに、顧客が増えるか減るかどうかはそのイベントの中身が決まるまでわからないという、なんだかシュレディンガーの猫みたいな話ですが、問題はどうやって中身を決めるかです。ここで確率を使います。

例えば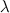と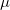が同じ値であると仮定してみます。シミュレーション中はArrivalとDepartureが同じ頻度で発生するのですから、あるイベントが発生した時にArrivalである確率は50%であると簡単にわかります。それでは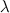が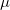の2倍だったら? 2/3でほぼ66.7%ですね。このように、Arrivalが起こる確率は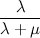で計算できます。例外は列に誰も並んでいないときで、この時発生したイベントは100%でArrivalです。

というわけで、モンテカルロ・シミュレーションを用いて待ち行列をシミュレートするのは次のようになります。

1. イベント発生。
2. もし顧客の数が0だったら、確実にArrivalなので顧客の数を1つ増やす。5.へ。
3. そうでなければ乱数生成器を使って(0,1)の乱数xを発生させる
4. もしxが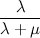より大きければ、Departureなので顧客の数を一つ減らす。そうでなければ、一つ増やす。
5. 1.に戻る。適当な数のイベントを発生させたら終了。

ところで、今回の目的はブロック率を求めることです。ブロック率はブロックされた数をArrivalの総数で割ればいいので2つのカウンターを用意しました。その名もarrivalとrejectionです。arrivalはArrivalが発生したときにインクリメントされ、rejectionはArrivalが発生し、かつ待ち行列が満杯(つまりN=5)の時にインクリメントされます。小数点以下第4位まで欲しかったのでArrivalを10000個発生させた時点で終了とします。Javaで書くと次のようになります。

public static void main(String[] args) {
    int N = 0; // 顧客数
    int lambda = 10; 
    int mu = 2; 
    int arrival = 0;
    int rejection = 0;

    Random r = new Random();    
    while (arrival < 10000) { // イベント発生
        if (N == 0) { // 確実にArrival
            arrival++;
            N++;
            continue;
        }
        double p = r.nextDouble();
        if (p > (double) lambda / (lambda + mu)) { 
            // Departure
            N--;
            continue;
        }
        arrival++;
        if (N == 5) { // キューが満杯なのでブロック
            rejection++;
        } else {
            N++;
        }
    }
    System.out.println((double) rejection / arrival);
}

実行すると大体0.800ほどの値が得られます。これは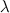が5、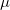が2、行列の上限が5の理論値(0.80005…)ともほぼ一致します(理論値を求める方法はまたの機会にします)。つまり、モンテカルロ・シミュレーションを用いて、ある待ち行列モデルのブロック率を求めることに成功しました。

まとめ

この記事ではモンテカルロ・シミュレーションを紹介しました。モンテカルロ・シミュレーションは乱数と確率のみを用いたシミュレーションで、有名なところでは円周率πの近似値を求めたりするのに使われます。

これを待ち行列に応用するには、顧客が並ぶ(Arrival)、離れる(Departure)といったイベントの頻度を使ってそれぞれのイベントの発生確率を計算します。次に、あるイベントが発生したと仮定して、そのイベントを乱数発生器を用いて確定します。その確定したイベントにしたがって待ち行列の状態を変化させます。

この手法のメリットの一つとして、プログラムを簡潔にすることができます。時間を軸にしたシミュレーションでは、シミュレーションクロックなどを用いて時間の流れを管理しなければならないからです。モンテカルロ・シミュレーションではシミュレーションクロックを完全に取り除くことができます。

その一方でデメリットとして時間を元にしたメトリクスを記録することが難しくなることが上げられます。例えば顧客の平均待ち時間などです。