正規表現が正しいことを数学的帰納法で証明する(その1)

自分がTAをやっている理論系のクラスの宿題から、多くの学生がつまづいていたところを紹介解説してみます。問題をかいつまんで言うと

アルファベットa、bからなる文字列のうち、aが偶数個ある文字列にマッチする正規表現を示し、それが正しいということを証明せよ。

用語について英語日本語間の対訳は適当なのでご了承下さい。原文も並べて書きたいのですがそれはまずいかもなんでやめときます。

この記事ではMathJaxを利用して数式等を表示しています。環境によってうまく表示されない場合はパソコンやスマホのwebブラウザで表示してみてください。

いくつかマッチする正規表現がありますが、とりあえず$(b\cup ab^*a)^*$としておきます。DFAやNFAもそうですが、正規表現を構築するには多少のひらめきが必要だったりします。

2つの言語$A$と$B$が等価であることを示すには$A\subseteq B$かつ$B\subseteq A$であることを両方示さないといけません。ここでは正規表現を$R$、aが偶数個あるような文字列の集合を$L$とします。

ステップ1

まずは$R\subseteq L$です。そもそも$R\subseteq L$とはどういうことなのでしょうか？$R$と$L$はそれぞれ集合なのでベン図を書いてみます。

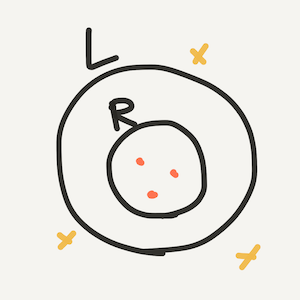
Venn diagram

すると$R\subseteq L$を示すには

$R$の中にあるものが$L$の中にもある($w\in R\Rightarrow w\in L$)か、その対偶
$L$の中にないものが$R$の中にもない($w\not\in L\Rightarrow w\not\in R$)

のどちらかを示すことができれば良さそうです。どちらを示すかはケースバイケースです。

$w\in R\Rightarrow w\in L$ということはつまり具体的に言うと、「正規表現にマッチする文字列はaが偶数個ある」ということです。「正規表現にマッチする文字列」というのを表現しなければいけないので数学的帰納法で証明しましょう。

命題

$w\in (b\cup ab^*a)^*$より$w$が0以上の$(b\cup ab^*a)$からなることがわかるので、命題を「$n$個の$(b\cup ab^*a)$にマッチする文字列はaが偶数個ある」としてみます。

Base case

まずは$n=0$の時にこの命題が成り立つことを証明します。

$$w^0\in (b\cup ab^*a)^0=\epsilon$$

ということで空文字$\epsilon$は明らかにaが偶数個の文字列ですね。

Induction step

ここで、$n=k$の時にこの命題が成り立つと仮定します。つまり「$k$個の$(b\cup ab^*a)$にマッチするような文字列$w^k$はaが偶数個ある」です。この仮定するところが数学的帰納法の肝かつややこしいところなのですが、ここでは置いておきます。で、この時に$n=k+1$に対してこの命題が成り立つことを証明すればいいわけです。

$w^{k+1}\in (b\cup ab^*a)^k(b\cup ab^*a)$ですが、ここでわかることは$w^k$の後で$b$か$ab^*a$のどちらかがマッチするということです。

もし$b$がマッチした場合、その文字列のaの数は増えていないことになります。一方$ab^*a$がマッチすると、aの文字数は2個増えたということになります。どちらにしても仮定より$w^k$は偶数個のaを含んでいるのですから$w^{k+1}$に含まれるaの数も偶数個であると結論付けることができます。

結論

上記より全ての$n\ (n\geq0)$において$n$個の$(b\cup ab^*a)$にマッチする文字列はaが偶数個ある」という命題が成り立つということを証明できました。

ここまで出来てようやく半分です。

ステップ2

では次に$L\subseteq R$を証明しましょう、としたいところですが、だいぶ長くなってしまったので次回の記事にしようと思います。是非皆さんも考えてみてください。「aが偶数個の文字列」というのをどう表すかが微妙に混乱したりします。

ついでにこの授業で使ってる教科書(の日本語版)をはっておきます。この本は状態遷移図から始まってチューリングマシンとNP問題にたどり着くんですが、アルゴリズムの方から考えるNP問題とは結論が同じだとしても視点が全く異なるので新鮮かつ、こっちの方がしっくり来るという人もいるかと思います。自分は結構好きです。