再帰関数の末尾再帰(最適化)について

関数の再帰と末尾再帰について学習したのですが、ちょうど某所で話題にあがってたので良いタイミングだなと思って書き留めておきます。

再帰とは自分自身を参照するようなアクションのことです。再帰関数が一番に思い浮かびますが、定義や言葉遊びなどでも使われます。例えばプログラム言語のPHPですが、この頭文字は現在「PHP: Hypertext Preprocessor」を意味するものとなっています。PHPを展開したのにまたPHPが出てきます。

階乗を計算する!

さて自分自身を呼び出す関数のことを再帰関数と呼びますが、一例としてnの階乗を計算する関数を見てみましょう。nの階乗とはn!と書き、1からnまでを乗算した数です。1の階乗は1、2の階乗は1×2で2、3の階乗は1×2×3で6となります。同様に、nの階乗は1×2×…×(n-1)×nとなります。

もうちょっと詳しく計算を注目してみます。

• 1! = 1
• 2! = 1×2 = 1!×2
• 3! = 1×2×3 = 2!×3
• …
• n! = 1×2×…×(n-1)×n = (n-1)!×n

nの階乗は(n-1)の階乗にnを掛けたもの、ということがわかるので(n-1)の階乗を計算しようとします。そのためには(n-1)-1の階乗、つまり(n-2)!が必要です。そうやって一つ手前の階乗を順番に計算していって、最終的に1の階乗に来た時にやっと1!が1であることにたどり着きます。階乗を計算するのに階乗が必要になる、立派な再帰ですね。まとめると、

• 1! = 1
• n! = n × (n-1)!

階乗の定義はこれだけです。簡単ですね。nの階乗を求めたいときには、nが1だったら1を、それ以外だったら(n-1)の階乗を計算してそれにnを掛けたものを返します。これをJavaで書くと次のようになります。

public int factorial(int n){
    if(n == 1) return 1;
    else return n * factorial(n-1);
}

このように再帰関数は定義をそのまま表したものによく似ていることが多く、見た目にも何をしているのかわかりやすいのが特徴です。もう一つの例を見てみましょう。

フィボナッチ数

フィボナッチ数列は以下のように定義されます(一例)。

• 1番目の数は1
• 2番目の数も1
• n番目の数は(n-1)番目と(n-2)番目の数を足したもの

実際に計算してみると、1、1、2、3、5、8、13、…と続きます。そこでn番目の数を計算するプログラムはこうなります。

public int fib(int n){
    if(n == 1) return 1;
    else if(n == 2) return 1;
    else return fib(n-1) + fib(n-2);
}

イメージ通りだったでしょうか。

効率を考える

見た目もシンプルでわかりやすい再帰関数ですが、プログラム中で利用するにはいくつか問題があります。その内の一つが再帰から戻ってくるためにコールスタックを一つ消費する必要があるということです。

コールスタックとは新たな作業を始めるためのスペースだと思ってください。人が並んで座れる長机だと考えるとわかりやすいかもしれません。このスペースがなくなるまで(つまり、隣に人が座れなくなるまで)再帰を続けるとスタックオーバーフローというエラーが起こります。このため無限に再帰関数を呼び続けることはコールスタックに制限がある以上簡単にはできません。

もうちょっと具体的にみてみます。さっきのfactorial関数ですが、nを計算するときに(n-1)の階乗の結果を待たなければなりません。このため、この関数はコールスタックを一つ消費して(n-1)!を計算しようとします。座ってる机の隣のスペースにに人を呼んで仕事を頼む感じです。

(n-1)!を頼まれた人は、また別の人を呼んで(n-2)!の計算を頼みます。このように次々に仕事を次の人に頼んでいき、最終的に1!の計算を頼まれた人が1を計算結果として2!を計算しようとしている人に返します。すると2!の人は、返ってきた1と2を掛けた2を計算結果として3!の人に返します。このようにして次々と結果が返ってきて、最終的にはn!の人が(n-1)!の人から返ってきた結果にnを掛けて計算終了となります。

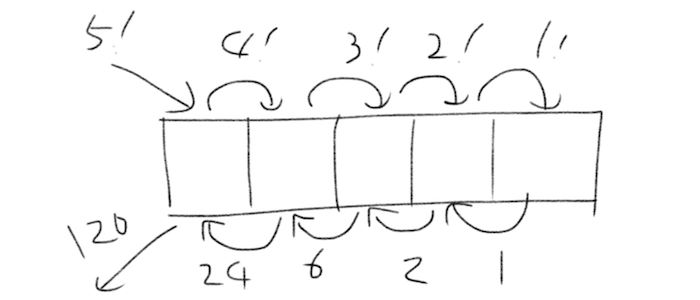
このやり方ですと100!を計算しようとすると100人が必要になることになります。さらに最初に仕事を頼んだ人は99!の人が計算を返すまでずっと待っていなければなりません。このような再帰は少し効率が悪そうに見えます。

隣の人に計算を投げっぱなしにする

ここで発想の転換を行います。頼んだ仕事が返ってくるのを待つのではなくて、自分の仕事を終わらせた後、隣に人を呼んで、後の作業を任せてしまうのです。任せてしまった後は自分は席を立って構いません。

このようにすれば、計算中に同時に長机に座っている人は一人だけです。いくら再帰を呼んでもコールスタックを消費しないので無限に再帰することができます。これが末尾再帰の概念です。

さて実際どのようにfactorial関数を末尾再帰にするかを考えます。最初の人が頼んだ計算結果を待たなければいけない理由は再帰を呼ぶ式に理由があります。関数の2行目を見てみましょう。

else return n * factorial(n-1);

作業を完了するには、返ってきた計算結果にnを掛ける必要があるので待っているわけです。ここを投げっぱなしにするにはどうすればいいでしょうか。勘の良い人は、関数を呼ぶだけにすればいいと気がつくかもしれません。つまり

else return factorial(...);

だけにするのです。こうすれば、最初の人は「あとはよろしく」と隣の人に任せて 席をたつことができます。戻ってきたところで自分は何もすることがないですし。問題は...の部分をどうするかです。どうすれば隣の人に自分が計算した分を渡すことができるでしょうか。末尾再帰では補助変数としてaccumulatorというものがよく使われます。長机の例で言うなら、隣の人に渡す作業メモにそれまでの結果を書き記すようなものです。このaccを使ってfactorial関数を末尾再帰にしてみます。

public int factorial(int n, int acc){
    if(n == 1) return acc;
    else return factorial(n-1, acc*n);
}

違いが分かりますか？この関数は2つの変数を受け取るようになっています。ひとつは今までどおり計算対象のn、もうひとつはaccです。さらに関数の2行目に注目してください、return文が再帰呼び出しだけになっています。これなら隣の人に任せて自分は席をたつことができます。

ロジック

なるほど見た目は確かに末尾再帰になっているみたいですが、果たして計算結果は正しいのでしょうか。ちょっとロジックを見てみます。この関数はfactorial(n,1)のようにして呼び出します。

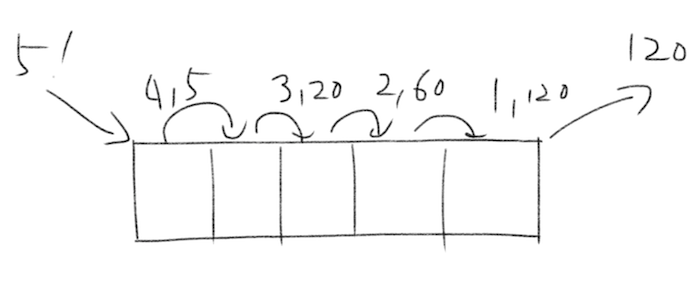
まずnが1の時を考えると、この関数はaccを直接返します。つまりfactorial(1,1)=1となり、これは正しいです。それではfactorial(2,1)はどうでしょうか。nは1ではないので、関数はfactorial(1, 2)を呼び出します。今度はnが1なのでaccである2を返します。うん、あってる。factorial(3, 1)のときは再帰呼び出しはfactorial(3, 1)->factorial(2, 3)->factorial(1, 6)となります。これも正しい。

accだけに注目してみましょう。nが1つずつ減っていくたびに、accにはその時のnが掛けられます。最初はn、その次はn-1、その次はn-2という風に。なんだか階乗の計算を逆からやっているような感じですが、実際その通りです。

再帰とループ

プログラムを勉強したことがある人は、再帰とループはいつでも相互に変換可能であると聞いたことがあると思います。再帰呼び出しをループに変換してしまえばもちろんコールスタックは消費しないので、いつまでもループすることができます。この点で末尾再帰とループ変換は同じ方向を向いていると言えます。末尾再帰が隣の人に作業を頼むなら、ループ変換は一人で黙々と計算し続けるイメージです。

ところがいくつかのプログラム言語にはループが言語仕様として定められていない、あるいは煩雑であるようなものがあります。関数型言語がいい例です。そのため末尾再帰がより利用され、そのようなコンパイラも末尾再帰の最適化をサポートしています。しかし、ここまでの例で使っておいてなんですが、Javaのコンパイラは残念ながら末尾再帰の最適化をサポートしていません。

まとめ

今回は末尾再帰を学習しました。末尾再帰とはプログラミングにおける再帰呼び出しの一種で、コンパイラの最適化によってはコールスタックを消費しないためネストが深くなりがちの再帰処理に向いています。末尾再帰になる条件は「再帰呼び出しを行う行がreturnと関数呼び出しだけで構成されていること」です。