機械学習： linear regression (1)

機械学習と聞いて思い浮かぶことはニューラルネットワークだとかフィードバックループだとか、面白そうだけどなんだか難しいんじゃないの？という感じでした。しかし講義を聞いてみると基礎の部分は以外とシンプルなことがわかりました。

ツッコミ大歓迎です。

機械学習の目的をものすごく簡単にいうと、「学習データを用いて未知のデータを分類できるようにする」ということです。例えば、過去の天気データをもとに明日の天気を予測するとか、あるいは過去の顧客データをもとに商品Aを買った人は商品Bも買う可能性が高いから推薦しようとかです。

根本的なところは未知のデータxから分類データyを導くような関数f(x)を探せればいいことになります。一番簡単な例からから始めてみます。誰もが一度はIQテストで次のような問題を見たことがあるはずです。

この場合f(x)はx(x-1)とできます(一例です)。このような問題では大抵見当がつくようになっていますが、まったく見当がつかなかったらどうすればいいでしょうか？例えば次のテーブルをみてください。

#	走行距離 (km)	売値 ($)
1	100,000	10,000
2	80,000	11,000
3	150,000	6,000
4	75,000	10,500
...	...	...
n	110,000	8,500

これはあなたが売りたい車の走行距離と売値に関する過去データの一部です。あなたの目的は現在の走行距離から適切な売値を計算することです。少なくとも計算された値より高値で買い取ってもらいたいものです。

走行距離をx軸、売値をy軸にとったグラフを書いてみると、走行距離が長ければ長いほど、売値が低くなっているのでなんとなく負の相関がありそうです。計算を簡単にするためにf(x)は1次関数、いわゆるy=ax+bで表せられるような式であると仮定してみます。どうすれば適切なaとbを見つけることができるでしょうか。

一つの方法としてはaとbをしらみつぶしに試すことができます。例えばaを-0.01、bを15000などとして、それぞれのデータを当てはめてみて売値が一致するかを見ます。一致するかどうかを測るのに予想値から実際の売値を引いて2乗したもののトータルを使うことにします。一致したならトータルが0になりますし、その値が小さければ小さいほど良い値だということになります。ということで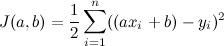が最小になるようなaとbを探します。後々のために1/2を掛けておきます。

ただし、しらみつぶしにaとbを探すのは効率が悪すぎます。そこでJ(a,b)が2次関数であることを利用してその微分が0になるところ、つまりグラフの底を見つけることにします。aとbそれぞれについて微分します。

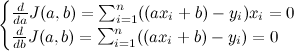
変換すると

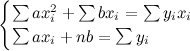
となります。データの個数n及び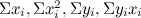は過去データから計算できるので未知なのはaとbだけ、2つの式があるので連立方程式として解くことができます。これで過去データからf(x)=ax+bの近似式に必要なaとbを導くことができました。これも立派な機械学習です。思っていたよりもややこしくないような気がしませんか？

もちろん現実には走行距離だけで売値が決まるとは限りませんし、実際の式が1次関数であるとも限りません。それでも一歩ずつ進んでいくために、次の記事では評価軸がたくさんある場合の1次関数の近似式を計算してみることにします。